面向未来电动汽车的技术：具有容差的全新变压器设计

    为了在高性能细分领域持续达到良好的效率水平，我们需要具有低开关损耗的功率开关组件。现代产品经常使用谐振转换器拓扑结构，该结构利用了零电压开关原理(zero voltage switching, ZVS)，优势是减少开关损耗。它们  常出现在LLC 谐振转换器中，其电路中的谐振电感可实现零电压开关，使得LLC 器件非常适合要求高效率及大功率的车载充电器(OBC)应用。

    LLC 一词指的是谐振电路依赖的三个组件功能：变压器励磁电感(Lm)、变压器漏感(Lr) 和谐振电容(Cr)。如果数值计算正确且遵守所需的  容差(tolerance)，这是使用LLC 变压器漏感来取代所需谐振电感的已知方法。供货商普思电子(Pulse Electronics) 使用有限元模型分析法(finite element modeling) 设计了一款3.6 kW 的LLC 变压器，具备高及  容差的漏感，能够作为LLC 转换器的谐振电感。

    针对这款3.6 kW LLC 变压器开发的系统要求包括：次级侧对初级侧的匝数比(N) 是2，初级侧的励磁电感是36 μH，的变压器增益( 放大倍数) 为6。

    结果显示放大倍数与变压器的初级绕组漏感(leakage inductance) 直接相关。因此，为了实现的放大倍数，这个寄生参数需要设有  容差。为了实现这个目标，要使用一项创新的变压器设计。

    图1 所示为LLC 电路框图，其中的突出部分是谐振电感Lr。谐振电路与输出/ 平滑电路产生电感耦合。

    图1 具备理想变压器模型的LLC转换器

    磁力耦合主要由线圈结构和铁芯气隙(air gap) 的几何形状决定。

    我们使用以下公式得出LLC 转换器的放大倍数：

    放大倍数＝ (Lm + Lr) / Lr    (1)

    励磁电感Lm 的容差值可以通过严格遵守铁芯气隙的容差值来控制，但谐振电感Lr 则需要进一步研究。

    图2 提供了更加完整的模型，这个模型包括了初级侧线圈的漏感(Lk_prim) 和次级侧线圈的漏感(Lk_sec)，以及可能出现的外部谐振电感(Lext)。

    图2 示意漏感的变压器电路

    接下来就清楚了：

    Lr = Lext + Lk_prim   (2)

    如前所述，通过设计具有足够大漏感的变压器，可以省去外部谐振电感器。这里的挑战在于为这项寄生参数设定合适的严格容差，而普思电子正是以一项新颖的线圈设计达成了这个目标。

    1   夹心绕法的线圈设计

    一个示例是PQ50/50 平台，它的初级侧和次级侧线圈导线的尺寸正好适用于3.6 kW 功率水平。考虑到变压器开发目标的系统要求，决定漏感值的式(1)和式(2) 说明了“将初级侧线圈和夹心式绕法的次级侧侧线圈彼此分立的设计，  接近目标值”。

    图3 显示了用于微调漏感值的线圈设计截面图。这个设计的独特之处在于能够各自独立控制线圈之间的距离，并达到所需的漏感值。每个线圈的宽度和线束尺寸都经过仔细调整，以适应线圈，将其微调到符合漏感容差要求。

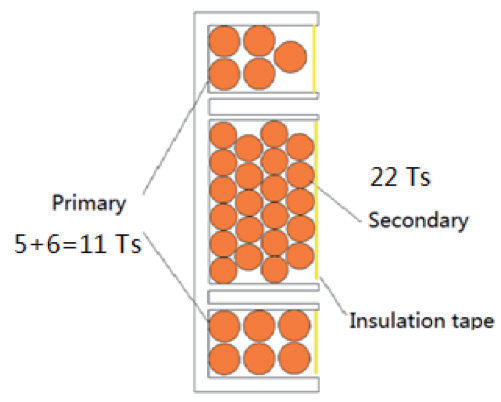
    图3 用于微调漏感值的线圈设计截面图

    2   优化变压器设计的有限元法

    为了  终完成设计并确保漏感集中在初级侧线圈周围，必须优化初级侧和次级侧线圈的设计以及铁芯气隙的位置。

    该设计是以有限元法建立模型所开发的，有限元法是一种用于分析技术性磁力问题并开发有效解决方案的现代方法。所产生的磁通达到了预期结果。图4显示了初级侧线圈和次级侧线圈各个磁通路径的有限元模型。

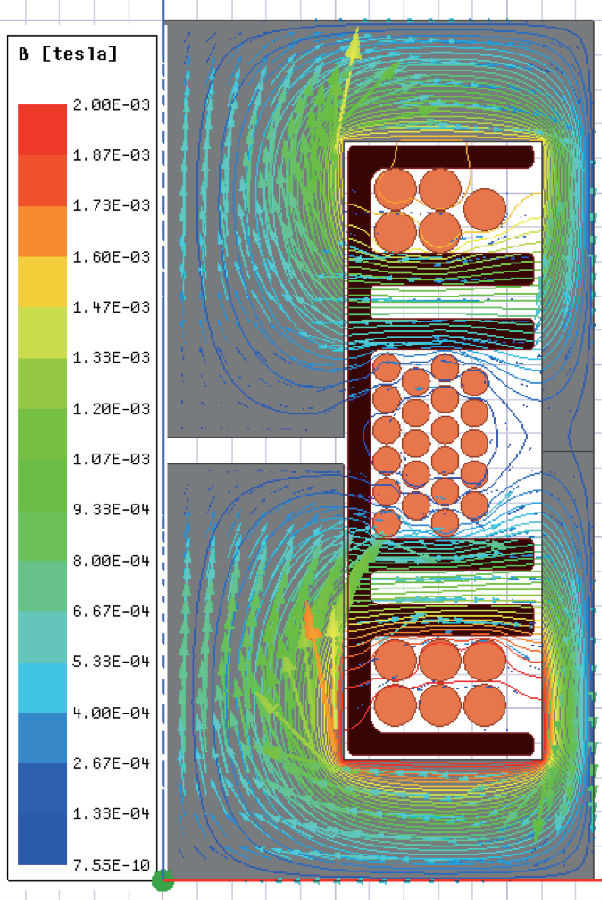
    图4 初级侧线圈(左)和次级侧线圈(右)各个磁通路径的有限元法分析模型

    原型设计( 图5) 和电气测试证实了优化变压器设计的有限元模型仿真结果。

    电气参数的测量结果显示，已经达到目标漏感值和容差值。

    为了计算实际的初级和次级绕组漏感，我们测量以下变压器参数：

    Lso：次级侧在开路状态时的初级侧电感

    Lss：次级侧在短路状态时的初级侧电感

    Lpo：初级侧在开路状态时的次级侧电感

    另外使用三个等式来计算初级侧的漏感(Lk_prim)，次级侧的漏感(Lk_sec)，以及励磁电感(Lm) 等数值。

    Lk_prim = Lso – Lm   (3)

    Lk_sec = Lpo - Lm×N 2   (4)

    Lm = SQRT ((Lso-Lss)×Lpo/N 2)   (5)

    表1 总结了变压器的测量和计算结果。初级绕组的励磁和漏感参数值圆满达到目标，次级侧的漏感值则相对较低。

    而且，该结果还证实了次级绕组的漏感已经有效地  化，并且通过小信号分析可以将漏感集中在初级侧。理论上，在变压器的一个绕组上产生的感应电压是匝数比乘以施加到另一绕组的电压，如下所示：

    Vout = N×Vin&